4 Uni- und Bivariate Datenanalyse
In diesem Kapitel behandeln wir die gängigsten Verfahren zur uni- und bivariaten Datenanalyse und wie diese in den verwendeten Ökosystemen umgesetzt sind. Damit kann sich ein Überblick über die Datenstruktur verschafft und erste Zusammenhänge überprüft werden. Zur Veranschaulichung dieser Analyseschritte werden am Ende dieses Kapitels erste vereinfachte Möglichkeiten angeboten, diese grafisch aufzubereiten.
4.1 Gewichtung
Sozialwissenschaftlich arbeiten wir vielfach mit Umfragedaten, mit denen Aussagen über eine größere Grundgesamtheit gemacht werden sollen (wie bspw. der in den Beispielen verwendete Allbus-Datensatz). Diese Daten beinhalten aber oft Verzerrungen (gewollt (Oversample) oder ungewollt (Non-Response)), welche ihre Repräsentativität einschränken. Um diesem Problem zu begegnen, ist es erforderlich die Daten zu gewichten. Bei der Auswahl der Codes, welche wir für die einzelnen Analyseschritte für dieses e-Book zusammengestellt haben, haben wir daher durchgehend darauf geachtet, dass die Verfahren gewichtet möglich sind.
Hinweis an bisherigen SPSS-Nutzer:innen: Die Gewichtung erfolgt in R für jede Analyse einzeln (und nicht einmal für die ganze Analyse-Session wie in SPSS). Bei jedem Analyseschritt muss daher angegeben werden, ob gewichtet werden soll.
Die Gewichtung erfolgt bei den einzelnen Funktionen i.d.R. mit dem Argument weights=. Bei jeder Funktion ist dies aber noch einmal ausgewiesen.
4.2 Univariate Statistiken
Für univariate Statistiken haben wir die gängigsten Verfahren zusammengestellt (Häufigkeitsverteilungnen sowie Lage- und Streuungsmaße).
| Packet | Funktion | Verwendung |
|---|---|---|
| sjmisc | frq() | Häufigkeitstabelle |
| sjmisc | descr() | Despriptive Statistiken ausgeben |
| sjstats | weighted_mean() | Mittelwert berechnen |
| sjstats | weighted_median() | Median berechnen |
| sjstats | weighted_sd() | Standardabweichung berechnen |
| sjstats | weighted_se() | Standardfehler berechnen |
| weights | wtd.quantile() | Quantile berechnen |
Frq()
Mit der Funktion frq() können Häufigkeitstabellen ausgegeben werden, welche die Informationen: Value, Valuelabel, N, RaW %, Valid % und CUm. % umfassen. (Sie entsprechen damit dem SPSS-oUtput).
Syntax:
# Ohne Pipe
frq(datensatz$variable1, weights = datensatz$gewicht)
# Mit Pipe
datensatz %>%
frq(variable1, weights = gewicht)Beispielcode:
# Häufigkeitstabelle Leistungsprinzip (im19)
allbus2018 %>% frq(im19, weights = wghtpew)
#> EINKOMMENSDIFFERENZ ERHOEHT MOTIVATION (im19) <numeric>
#> # total N=3370 valid N=3370 mean=2.49 sd=0.93
#>
#> Value | Label | N | Raw % | Valid % | Cum. %
#> --------------------------------------------------------------
#> 1 | STIMME VOLL ZU | 532 | 15.79 | 15.79 | 15.79
#> 2 | STIMME EHER ZU | 1186 | 35.19 | 35.19 | 50.98
#> 3 | STIMME EHER NICHT ZU | 1132 | 33.59 | 33.59 | 84.57
#> 4 | STIMME GAR NICHT ZU | 520 | 15.43 | 15.43 | 100.00
#> <NA> | <NA> | 0 | 0.00 | <NA> | <NA>Descr()
Mit descr() werden die wesentlichen deskriptiven Statistiken ausgegeben: prozentuale Angabe fehlender Werten, Mittelwert, Standardabweichung, Standardfehler, Wertebereich, Interquartilsabstand, Scheife.
Syntax:
# Ohne Pipe
descr(datensatz$variable1, weights = datensatz$gewicht)
# Mit Pipe
datensatz %>%
descr(variable1, weights = gewicht)Mit dem Argument show = "short" wird die Ausgabe verkürzt und nur noch: prozentuale Angabe fehlender Werten, Mittelwert, Standardabweichung ausgegeben.
Beispielcode:
# Deskriptive Statistiken Leistungsprinzip (im19)
allbus2018 %>% descr(im19, weights = wghtpew)
#>
#> ## Basic descriptive statistics
#>
#> var type label n NA.prc mean sd se
#> im19 numeric EINKOMMENSDIFFERENZ ERHOEHT MOTIVATION 3370 2.99 2.49 0.93 0.02
#> range iqr skew
#> 3 (1-4) 1 0.01
allbus2018 %>% descr(im19, weights = wghtpew, show = "short")
#>
#> ## Basic descriptive statistics
#>
#> var n NA.prc mean sd
#> im19 3370 2.99 2.49 0.93Weighted_mean()
weighted_mean() wird verwendet um lediglich den Mittelwert zu berechnen. Dies hat den Vorteil, dass das Ergebnis direkt als neue Variable abgespreichert werden kann (siehe dazu den Beispielcode unten).
ACHTUNG: In der Pipe-Schreibeweise muss hier der %$%-Operator verwendet werden.
Syntax:
# Ohne Pipe
weighted_mean(datensatz$variable1, weights = datensatz$gewicht)
# Mit Pipe
# Achtung! %$% Operator
datensatz %$%
weighted_mean(variable1, weights = gewicht)Beispielcode:
# Mittelwert Leistungsprinzip (im19)
allbus2018 %$%
weighted_mean(im19, weights = wghtpew)
#> [1] 2.48678
# Mittelwert Leistungsprinzip (im19) als neue Variable
ds <- allbus2018 %>%
transmute(mittelLeistung = weighted_mean(im19, weights = wghtpew))
ds
#> # A tibble: 3,477 × 1
#> mittelLeistung
#> <dbl>
#> 1 2.49
#> 2 2.49
#> 3 2.49
#> 4 2.49
#> 5 2.49
#> 6 2.49
#> 7 2.49
#> 8 2.49
#> 9 2.49
#> 10 2.49
#> # … with 3,467 more rowsWeighted_median()
Analog zur vorherigen Funktion wird mit weighted_median() nur der Median berechnet.
ACHTUNG: In der Pipe-Schreibeweise muss hier der %$%-Operator verwendet werden.
Syntax:
# Ohne Pipe
weighted_median(datensatz$variable1, weights = datensatz$gewicht)
# Mit Pipe
# Achtung! %$% Operator
datensatz %$%
weighted_median(variable1, weights = gewicht)Beispielcode:
# Median Leistungsprinzip (im19)
allbus2018 %$%
weighted_median(im19, weights = wghtpew)
#> [1] 2
# Median Leistungsprinzip (im19) als neue Variable
ds <- allbus2018 %>%
mutate(medianLeistung = weighted_median(im19, weights = wghtpew)) %>%
distinct(medianLeistung)
ds
#> # A tibble: 1 × 1
#> medianLeistung
#> <dbl>
#> 1 2Weighted_sd()
Mit weighted_sd kann die Standardabweichung berechnet werden.
ACHTUNG: In der Pipe-Schreibeweise muss hier der %$%-Operator verwendet werden.
Syntax:
# Ohne Pipe
weighted_sd(datensatz$variable1, weights = datensatz$gewicht)
# Mit Pipe
# Achtung! %$% Operator
datensatz %$%
weighted_sd(variable1, weights = gewicht)Beispielcode:
# Mittelwert und Standardabweichung Leistungprinzip nach Ost-West (Fälle)
ds <- allbus2018 %>%
select(eastwest, im19, wghtpew) %>%
group_by(eastwest) %>%
mutate(leistungMittelOstWest = weighted_mean(im19, weights = wghtpew),
leistungSDOstWest = weighted_sd(im19, weights = wghtpew)) %>%
ungroup()
ds %>%
select(eastwest, leistungMittelOstWest, leistungSDOstWest)
#> # A tibble: 3,477 × 3
#> eastwest leistungMittelOstWest leistungSDOstWest
#> <dbl> <dbl> <dbl>
#> 1 1 2.46 0.923
#> 2 2 2.60 0.985
#> 3 1 2.46 0.923
#> 4 2 2.60 0.985
#> 5 2 2.60 0.985
#> 6 1 2.46 0.923
#> 7 1 2.46 0.923
#> 8 1 2.46 0.923
#> 9 1 2.46 0.923
#> 10 2 2.60 0.985
#> # … with 3,467 more rowsWeighted_se()
weighted_se() wird verwendet, um nur den Standardfehler zu berechnen.
ACHTUNG: In der Pipe-Schreibeweise muss hier der %$%-Operator verwendet werden.
Syntax:
# Ohne Pipe
weighted_se(datensatz$variable1, weights = datensatz$gewicht)
# Mit Pipe
# Achtung! %$% Operator
datensatz %$%
weighted_se(variable1, weights = gewicht)Beispielcode:
# Mittelwert, Standardabweichung und Standardfehler
# Leistungprinzip nach Ost-West (Gruppen)
ds <- allbus2018 %>%
select(eastwest, im19, wghtpew) %>%
group_by(eastwest) %>%
summarise(leistungMittelOstWest = weighted_mean(im19, weights = wghtpew),
leistungSDOstWest = weighted_sd(im19, weights = wghtpew),
leistungSEOstWest = weighted_se(im19, weights = wghtpew)) %>%
ungroup()
ds
#> # A tibble: 2 × 4
#> eastwest leistungMittelOstWest leistungSDOstWest leistungSEOstWest
#> <dbl> <dbl> <dbl> <dbl>
#> 1 1 2.46 0.923 0.0192
#> 2 2 2.60 0.985 0.0302
# Mittelwert, Standardabweichung, Standardfehler und .95 Konfidenzintervall
# Leistungprinzip nach Ost-West (Gruppen)
ds <- allbus2018 %>%
group_by(eastwest) %>%
summarise(leistungMittelOstWest = weighted_mean(im19, weights = wghtpew),
leistungSDOstWest = weighted_sd(im19, weights = wghtpew),
leistungSEOstWest = weighted_se(im19, weights = wghtpew),
CI.95.down = leistungMittelOstWest-1.96*(leistungSDOstWest/sqrt(n())),
CI.95.up = leistungMittelOstWest+1.96*(leistungSDOstWest/sqrt(n()))) %>%
ungroup()
ds
#> # A tibble: 2 × 6
#> eastwest leistungMittelOstWest leistungSDOstWest leistungSEOstWest CI.95.down
#> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 1 2.46 0.923 0.0192 2.43
#> 2 2 2.60 0.985 0.0302 2.55
#> # … with 1 more variable: CI.95.up <dbl>wtd.quantile()
Für die Berchnung der Quantile müssen wir auf das Paket weights zurückgreifen. Bitte installieren und laden. Wir verwenden davon die Funktion wtd.quantile.
ACHTUNG: In der Pipe-Schreibeweise muss hier der %$%-Operator verwendet werden.
library(weights)Syntax:
# Ohne Pipe
wtd.quantile(datensatz$variable1, weights = datensatz$gewicht)
# Mit Pipe
# Achtung! %$% Operator
datensatz %$%
wtd.quantile(variable1, weights = gewicht)Beispielcode:
# Quantile Alter
allbus2018 %$%
wtd.quantile(age, weights = wghtpew)
#> 0% 25% 50% 75% 100%
#> 18 36 52 65 954.3 Bivariate Statistiken
Für bivariate Statistiken schauen wir uns zunächst mit der Funktion crosstab() die gemeinsame Verteilung zweier Variablen in einer Kreuztabelle an. Die Zusammenhangsmaße können wir überwiegend mit crosstable_statistics() abrufen. Für den Chi-Quadart-Test und den Korrelataionskoeffizienten nach Pearson verwenden wir spezifisch dafür geschriebene Funktionen.
| Packet | Funktion | Verwendung |
|---|---|---|
| dscr | crosstab() | Kreuztabellen |
| sjstats | weighted_chisqtest() | Chi-Quadrat-Test |
| sjstats | crosstable_statistics() | Zusammenhangsmaße |
| sjmisc | weighted_correlation() | Pearson`s r |
Crosstab()
Für die Berechung einer Kreuztabelle verwenden wir das Paket descr, welches installiert und geladen werden muss.
library(descr)
# Achtung! Überschreibt sjmisc::descr
# Paket sjmisc deaktivieren und nochmal aktivieren
detach("package:sjmisc", unload = TRUE)
library(sjmisc)Syntax:
Mit der Funktion crosstab aus dem descr-Paket berechnen wir die Kreuztabelle. Mit der ersten Variable definieren wir die Zeilen und mit der Zweiten die Spalten. Im default ohne weitere Spezifikation erhalten wir eine Kreuztabelle mit den absoluten Häufigkeiten und eine Mosaik-Plot der Verteilung. Für andere Angaben müssen entsprechende Argumente benannt werden. Siehe dazu die folgenden Beispiele oder die Hilfeseite der Funktion mit ?crosstab.
ACHTUNG: In der Pipe-Schreibeweise muss hier der %$%-Operator verwendet werden.
# Ohne Pipe
crosstab(datensatz$variable1, datensatz$variable2, weights = datensatz$gewicht)
# Mit Pipe
# Achtung! %$% Operator
datensatz %$%
crosstab(variable1, variable2, weight = gewicht)Beispielcode:
# Kreuztabelle Geschlecht (sex) und Bildung (educ) -
# Absolute Häufigkeit
# ohne Grafik
allbus2018 %$%
crosstab(sex, educ, weight = wghtpew, plot = F)
#> Cell Contents
#> |-------------------------|
#> | Count |
#> |-------------------------|
#>
#> =================================================================================
#> ALLGEMEINER SCHULABSCHLUSS
#> GESCHLECHT, BEFRAGTE(R) 1 2 3 4 5 6 7 Total
#> ---------------------------------------------------------------------------------
#> 1 31 445 519 185 570 12 13 1775
#> ---------------------------------------------------------------------------------
#> 2 23 408 575 140 531 10 11 1698
#> ---------------------------------------------------------------------------------
#> Total 54 853 1094 325 1101 22 24 3473
#> =================================================================================
# Kreuztabelle Geschlecht (sex) und Bildung (educ) -
# relative Häufigkeit nach Spalten
# ohne Grafik
allbus2018 %$%
crosstab(sex, educ, weight = wghtpew, prop.c = T, plot = F)
#> Cell Contents
#> |-------------------------|
#> | Count |
#> | Column Percent |
#> |-------------------------|
#>
#> ========================================================================================
#> ALLGEMEINER SCHULABSCHLUSS
#> GESCHLECHT, BEFRAGTE(R) 1 2 3 4 5 6 7 Total
#> ----------------------------------------------------------------------------------------
#> 1 31 445 519 185 570 12 13 1775
#> 57.4% 52.2% 47.4% 56.9% 51.8% 54.5% 54.2%
#> ----------------------------------------------------------------------------------------
#> 2 23 408 575 140 531 10 11 1698
#> 42.6% 47.8% 52.6% 43.1% 48.2% 45.5% 45.8%
#> ----------------------------------------------------------------------------------------
#> Total 54 853 1094 325 1101 22 24 3473
#> 1.6% 24.6% 31.5% 9.4% 31.7% 0.6% 0.7%
#> ========================================================================================
# Kreuztabelle Geschlecht (sex) und Bildung (educ) -
# relative Häufigkeit nach Zeilen
# ohne Grafik
allbus2018 %$%
crosstab(sex, educ, weight = wghtpew, prop.r = T, plot = F)
#> Cell Contents
#> |-------------------------|
#> | Count |
#> | Row Percent |
#> |-------------------------|
#>
#> =====================================================================================
#> ALLGEMEINER SCHULABSCHLUSS
#> GESCHLECHT, BEFRAGTE(R) 1 2 3 4 5 6 7 Total
#> -------------------------------------------------------------------------------------
#> 1 31 445 519 185 570 12 13 1775
#> 1.7% 25.1% 29.2% 10.4% 32.1% 0.7% 0.7% 51.1%
#> -------------------------------------------------------------------------------------
#> 2 23 408 575 140 531 10 11 1698
#> 1.4% 24.0% 33.9% 8.2% 31.3% 0.6% 0.6% 48.9%
#> -------------------------------------------------------------------------------------
#> Total 54 853 1094 325 1101 22 24 3473
#> =====================================================================================
# Kreuztabelle Geschlecht (sex) und Bildung (educ) -
# relative Häufigkeit nach Gesamthäufigkeit
# ohne Grafik
allbus2018 %$%
crosstab(sex, educ, weight = wghtpew, prop.t = T, plot = F)
#> Cell Contents
#> |-------------------------|
#> | Count |
#> | Total Percent |
#> |-------------------------|
#>
#> ====================================================================================
#> ALLGEMEINER SCHULABSCHLUSS
#> GESCHLECHT, BEFRAGTE(R) 1 2 3 4 5 6 7 Total
#> ------------------------------------------------------------------------------------
#> 1 31 445 519 185 570 12 13 1775
#> 0.9% 12.8% 14.9% 5.3% 16.4% 0.3% 0.4%
#> ------------------------------------------------------------------------------------
#> 2 23 408 575 140 531 10 11 1698
#> 0.7% 11.7% 16.6% 4.0% 15.3% 0.3% 0.3%
#> ------------------------------------------------------------------------------------
#> Total 54 853 1094 325 1101 22 24 3473
#> ====================================================================================
# Kreuztabelle Geschlecht (sex) und Bildung (educ) -
# relative Häufigkeit mit Chi-Quadrat nach Zellen
# ohne Grafik
allbus2018 %$%
crosstab(sex, educ, weight = wghtpew, prop.chisq = T, plot = F)
#> Cell Contents
#> |-------------------------|
#> | Count |
#> | Chi-square contribution |
#> |-------------------------|
#>
#> ========================================================================================
#> ALLGEMEINER SCHULABSCHLUSS
#> GESCHLECHT, BEFRAGTE(R) 1 2 3 4 5 6 7 Total
#> ----------------------------------------------------------------------------------------
#> 1 31 445 519 185 570 12 13 1775
#> 0.419 0.188 2.880 2.150 0.095 0.051 0.044
#> ----------------------------------------------------------------------------------------
#> 2 23 408 575 140 531 10 11 1698
#> 0.438 0.196 3.010 2.247 0.099 0.053 0.046
#> ----------------------------------------------------------------------------------------
#> Total 54 853 1094 325 1101 22 24 3473
#> ========================================================================================
# Kreuztabelle Geschlecht (sex) und Bildung (educ) -
# relative Häufigkeit nach Spalten
# mit Chi-Quadrat-Test
# mit Grafik
allbus2018 %$%
crosstab(sex, educ, weight = wghtpew, prop.c = T, chisq = T, plot = F)
#> Cell Contents
#> |-------------------------|
#> | Count |
#> | Column Percent |
#> |-------------------------|
#>
#> ========================================================================================
#> ALLGEMEINER SCHULABSCHLUSS
#> GESCHLECHT, BEFRAGTE(R) 1 2 3 4 5 6 7 Total
#> ----------------------------------------------------------------------------------------
#> 1 31 445 519 185 570 12 13 1775
#> 57.4% 52.2% 47.4% 56.9% 51.8% 54.5% 54.2%
#> ----------------------------------------------------------------------------------------
#> 2 23 408 575 140 531 10 11 1698
#> 42.6% 47.8% 52.6% 43.1% 48.2% 45.5% 45.8%
#> ----------------------------------------------------------------------------------------
#> Total 54 853 1094 325 1101 22 24 3473
#> 1.6% 24.6% 31.5% 9.4% 31.7% 0.6% 0.7%
#> ========================================================================================
#>
#> Statistics for All Table Factors
#>
#> Pearson's Chi-squared test
#> ------------------------------------------------------------
#> Chi^2 = 11.91607 d.f. = 6 p = 0.0639
#>
#> Minimum expected frequency: 10.75612
# Grafik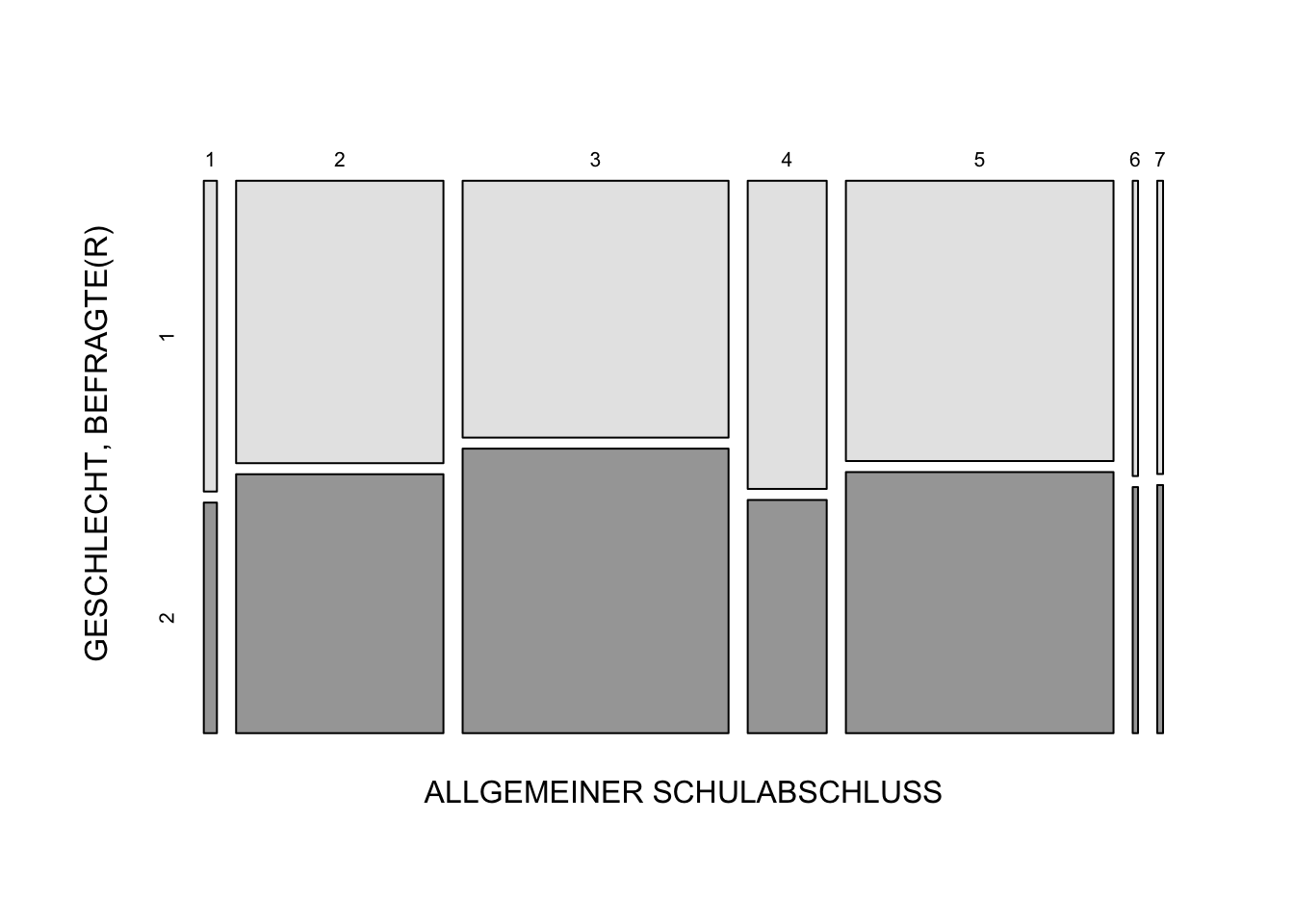
Weighted_chisqtest()
Der Chi-Quadrat-Test kann mit der crosstab-Funktion direkt unterhalb der Kreuztabelle berechnet oder direkt mit der weighted_chisqtest()-Funktion.
Syntax:
# Ohne Pipe
weighted_chisqtest(datensatz$variable1, datensatz$variable2, weights = datensatz$gewicht)
# Mit Pipe
datensatz %>%
weighted_chisqtest(variable1, variable2, weights = gewicht)Beispielcode:
# Chi-Quadrat-Test Geschlecht (sex) und Bildung (educ)
allbus2018 %>%
weighted_chisqtest(sex, educ, weights = wghtpew)
#>
#> # Measure of Association for Contingency Tables
#>
#> Chi-squared: 11.9161
#> Cramer's V: 0.0586
#> df: 6
#> p-value: 0.064
#> Observations: 3473Crosstable_statistiscs()
Die Funktion crosstable_statistics() können gängige Zusammenhangsmaße berechnet werden.
Syntax:
# Ohne Pipe
crosstable_statistics(datensatz$vaiable1, datensatz$variable2, weights = datensatz$gewicht,
statistics = c("phi", "cramer", "spearman", "kendall", "fisher"))
# Mit Pipe
allbus2018 %>%
crosstable_statistics(variable1, variable2, weights = gewicht,
statistics = c("phi", "cramer", "spearman", "kendall", "fisher"))Beispielcode:
# Phi Geschlecht (sex) und Ost West (eastwest)
allbus2018 %>%
crosstable_statistics(sex, eastwest, weights = wghtpew, statistics = "phi")
#>
#> # Measure of Association for Contingency Tables
#>
#> Chi-squared: 0.0769
#> Phi: 0.0055
#> df: 1
#> p-value: 0.781
#> Observations: 3477
# Cramers V Geschlecht (sex) und Bildung (educ)
allbus2018 %>%
crosstable_statistics(sex, educ, weights = wghtpew, statistics = "cramer")
#>
#> # Measure of Association for Contingency Tables
#>
#> Chi-squared: 11.9161
#> Cramer's V: 0.0586
#> df: 6
#> p-value: 0.064
#> Observations: 3473
# Spearman`s rho Leistungsprinzip (im19) und Befürwortung von Ungleichheit (im20)
allbus2018 %>%
crosstable_statistics(im19, im20, weights = wghtpew, statistics = "spearman")
#>
#> # Measure of Association for Contingency Tables
#>
#> S: 2913791351.3356
#> Spearman's rho: 0.5148
#> df: 9
#> p-value: < .001***
#> Observations: 3298Weighted_correlation()
Mit weighted_correlation berechnen wir den Korrelationskoeffizienten nach Pearson. Ausgeben wird der Wert des Korrelationskoeffizienten, die Werte für ein Konfidenzintervall von 95% in eckigen Klammern und der p-Wert,
Syntax:
# Ohne Pipe
weighted_correlation(datensatz$variable1, datensatz$variable2,
weights = datensatz$gewicht)
# Mit Pipe
datensatz %>%
weighted_correlation(variable1, variable2, weights = gewicht)Beispielcode:
# Pearson`s r Leistungsprinzip (im19) und Befürwortung von Ungleichheit (im20)
allbus2018 %>%
weighted_correlation(im19, im20, weights = wghtpew)
#>
#> Weighted Pearson's Correlation Coefficient
#>
#> estimate [95% CI]: 0.515 [0.493 0.536]
#> p-value: 0.0004.4 Mittelwertvergleiche (unabhängig)
Für Mittelwertvergleiche können mit folgenden Funktionen t-Tests, einfaktorielle ANOVAs und der Mann-Whitney-Test bzw. Kruskall-Wallis-Test berechnet werden.
| Packet | Funktion | Verwendung |
|---|---|---|
| sjstats | weighted_ttest() | T-Test |
| sjstats | grpmean() | Einfaktorielle ANOVA |
| sjstats | weighted_mannwhitney() | Mann-Whitney-Test / Kruskall-Wallis-Test |
Weighted_ttest()
Den t-Test berechnen wir mit der Funktion weighted_ttest(). Als Testergebnis werden der t-Wert, die Freiheitsgrade (df) und der P-Wert ausgegeben. Darunter wird der Mittelwert für beide Gruppen, die Mittelwertdifferenz sowie das 95%-Konfidenzintervall der Mittelwertdifferenz (in eckigen Klammern) ausgegeben.
Syntax:
# Ohne Pipe
weighted_ttest(variable1 ~ gruppenvariable + gewicht, datensatz)
# Mit Pipe
# Nicht gut zu handhaben!Beispielcode:
# T-Test zu Leistungsprinzip (im19) zwischen Geschlecht (sex)
weighted_ttest(im19 ~ sex + wghtpew, allbus2018)
#>
#> Two-Sample t-test (two.sided)
#>
#> # comparison of im19 by sex
#> # t=-6.06 df=3338 p-value=0.000
#>
#> mean in group [1] MANN: 2.393
#> mean in group [2] FRAU: 2.587
#> difference of mean : -0.195 [-0.257 -0.132]Grpmean()
Für einen Mittelwertvergleich über mehr als zwei Gruppen können wir mit der grpmean-Funktion eine einfaktorielle ANOVA berechnen. Ausgeben werden für jede Gruppe der Mittelwert, das N, die Standardabweichung, der Standardfehler sowie der p-Wert für den Mittelwertunterschied zum Mittelwert des gesamten Samples. Für die ANOVA werden der R-Quadrat-Wert, der korregierte R-Quadart-Wert, der F-Wert und der p-Wert ausgegeben.
Syntax:
# Ohne Pipe
grpmean(datensatz$variable1, datensatz$gruppenvariable, weights = datensatz$gewicht)
# Mit Pipe
datensatz %>%
grpmean(variable1, gruppenvariable, gewicht)
Beispielcode:
# Einfaktorielle Anova Leistungsprinzip (im19) zwischen Bildungsniveau (educ)
# P-Wert in Relation zu absolutem Mittelwert
allbus2018 %>%
grpmean(im19, educ, weights = wghtpew)
#>
#> # Grouped Means for EINKOMMENSDIFFERENZ ERHOEHT MOTIVATION by ALLGEMEINER SCHULABSCHLUSS
#>
#> Category | Mean | N | SD | SE | p
#> -------------------------------------------------------
#> OHNE ABSCHLUSS | 2.29 | 45 | 0.90 | 0.14 | 0.451
#> VOLKS-,HAUPTSCHULE | 2.20 | 817 | 0.92 | 0.03 | < .001
#> MITTLERE REIFE | 2.51 | 1058 | 0.94 | 0.03 | 0.080
#> FACHHOCHSCHULREIFE | 2.49 | 323 | 0.87 | 0.05 | 0.269
#> HOCHSCHULREIFE | 2.70 | 1081 | 0.91 | 0.03 | < .001
#> ANDERER ABSCHLUSS | 2.24 | 20 | 1.01 | 0.24 | 0.451
#> NOCH SCHUELER | 2.38 | 22 | 0.76 | 0.17 | 0.885
#> Total | 2.49 | 3370 | 0.93 | 0.02 |
#>
#> Anova: R2=0.041; adj.R2=0.039; F=23.736; p=0.000
# Einfaktorielle Anova Leistungsprinzip (im19) zwischen Bildungsniveau (educ)
# nach Geschlecht (sex)
# P-Wert in Relation zu absolutem Mittelwert
allbus2018 %>%
group_by(sex) %>%
grpmean(im19, educ, weights = wghtpew)
#>
#> Grouped by:
#> GESCHLECHT, BEFRAGTE(R): MANN
#>
#> # Grouped Means for EINKOMMENSDIFFERENZ ERHOEHT MOTIVATION by ALLGEMEINER SCHULABSCHLUSS
#>
#> Category | Mean | N | SD | SE | p
#> ------------------------------------------------------
#> OHNE ABSCHLUSS | 2.31 | 28 | 0.94 | 0.18 | 0.869
#> VOLKS-,HAUPTSCHULE | 2.15 | 435 | 0.89 | 0.04 | 0.103
#> MITTLERE REIFE | 2.45 | 506 | 0.93 | 0.04 | 0.076
#> FACHHOCHSCHULREIFE | 2.42 | 183 | 0.83 | 0.06 | 0.146
#> HOCHSCHULREIFE | 2.54 | 564 | 0.90 | 0.04 | 0.001
#> ANDERER ABSCHLUSS | 1.79 | 11 | 0.64 | 0.20 | 0.076
#> NOCH SCHUELER | 2.35 | 12 | 0.82 | 0.25 | 0.869
#> Total | 2.39 | 1733 | 0.91 | 0.02 |
#>
#> Anova: R2=0.030; adj.R2=0.026; F=8.815; p=0.000
#>
#>
#> Grouped by:
#> GESCHLECHT, BEFRAGTE(R): FRAU
#>
#> # Grouped Means for EINKOMMENSDIFFERENZ ERHOEHT MOTIVATION by ALLGEMEINER SCHULABSCHLUSS
#>
#> Category | Mean | N | SD | SE | p
#> -------------------------------------------------------
#> OHNE ABSCHLUSS | 2.24 | 17 | 0.85 | 0.22 | 0.323
#> VOLKS-,HAUPTSCHULE | 2.25 | 383 | 0.94 | 0.05 | 0.001
#> MITTLERE REIFE | 2.57 | 552 | 0.94 | 0.04 | 0.713
#> FACHHOCHSCHULREIFE | 2.58 | 139 | 0.92 | 0.08 | 0.713
#> HOCHSCHULREIFE | 2.87 | 517 | 0.89 | 0.04 | < .001
#> ANDERER ABSCHLUSS | 2.87 | 8 | 1.12 | 0.40 | 0.418
#> NOCH SCHUELER | 2.41 | 10 | 0.73 | 0.24 | 0.713
#> Total | 2.59 | 1637 | 0.95 | 0.02 |
#>
#> Anova: R2=0.060; adj.R2=0.056; F=17.300; p=0.000Weighted_mannwhitney()
Zur Berechnung des Mann-Whitney-Tests bzw. des Kruskall-Wallis-Tests verwenden wir die Funktion weighted_mannwhitney().
Syntax:
# Ohne Pipe
weighted_mannwhitney(variable1 ~ gruppenvariable + gewicht, datensatz)
# Mit Pipe
# Nicht gut zu handhaben!Beispielcode:
# Mann-Whitney-Test Leistungsprinzip (im19) nach Geschlecht (sex)
weighted_mannwhitney(im19 ~ sex + wghtpew, allbus2018)
#>
#> # Weighted Mann-Whitney-U test
#>
#> comparison of im19 by sex
#> Chisq=5.88 df=3371 p-value=0.000
# Kruskall-Wallis-Test Leistungsprinzip (im19) nach Geschlecht (sex)
weighted_mannwhitney(im19 ~ educ + wghtpew, allbus2018)
#>
#> # Weighted Kruskal-Wallis test
#>
#> comparison of im19 by educ
#> Chisq=6.00 df=130 p-value=0.0004.5 Grafiken
Zur grafischen Aufbereitung einiger der vorhergehenden univariaten und bivariaten Analysen bietet das Paket sjplot verschiedene Möglichkeiten an, mit wenigen Zielen Code Grafiken zu erstellen. Diese können exportiert und direkt in Ergebnisberichte verwendet werden.
| Packet | Funktion | Verwendung |
|---|---|---|
| sjplot | plot_frq() | Grafiken zu univariaten Häufigkeitsverteilungen |
| sjplot | plot_likert() | Grafiken zu univariaten Häufigkeitsverteilungen bei Likert-Items |
| sjplot | plot_stackfrq() | Grafiken als univariate Balkenschichtungsdiagramme |
| sjplot | plot_grpfrq() | Grafiken zu univariaten Häufigkeitsverteilungen nach Gruppen |
| sjplot | plot_xtab() | Grafiken als Kreuztabellendiagramme |
Plot_frq()
Mit der Funktion plot_frq() können verschiedene Grafiken zu univariaten Häufigkeitsverteilungen erstellt werden. Im default wird dabei ein einfaches Balkendiagramm erstellt, welches die absolute Anzahl der Befragten pro Kategorie sowie deren prozentualen Anteil an der Gesamtverteilung abbildet. Mit verschiedenen Argumenten (Übersicht mit ?plot_frq abrufbar) kann die Grafik entsprechend den eigenen Wünschen angepasst werden. In den Beispiele sind hierfür verschiedene Möglichkeiten aufgeführt.
ACHTUNG: In der Pipe-Schreibeweise muss hier der %$%-Operator verwendet werden.
Syntax:
# Ohne Pipe
plot_frq(datensatz$variable1, weight.by = datensatz$gewicht)
# Mit Pipe
# Achtung! %$% Operator
datensatz %$%
plot_frq(variable1, weight.by = gewicht)
Beispielcode:
# Grafik zur Häufigkeitsverteilung Bildung (educ)
allbus2018 %$%
plot_frq(educ, weight.by = wghtpew, coord.flip = T, hjust = "left", type = "dot",
show.ci = T, expand.grid = T, vjust = "bottom", sort.frq = "desc")
# Grafik zur Häufigkeitsverteilung Alter (age)
# mit Normalverteilungskurve, Mittelwert und Standardabweichung
allbus2018 %$%
plot_frq(age, weight.by = wghtpew, type = "h", show.mean = TRUE,
show.mean.val = TRUE, normal.curve = TRUE, show.sd = TRUE,
normal.curve.color = "black", geom.size = .3, xlim = c(15, 100))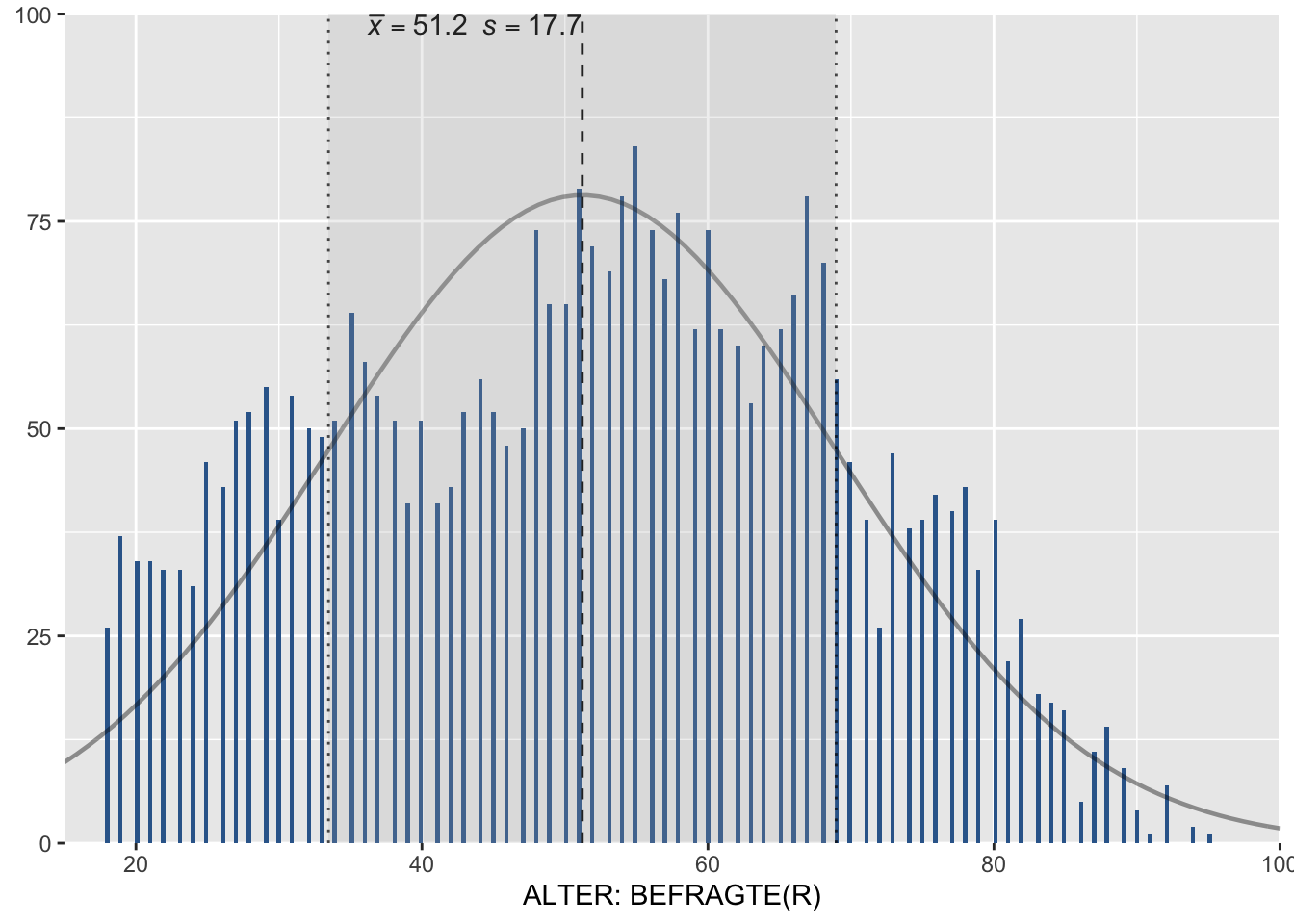
# Grafik zur Häufigkeitsverteilung Alter (age)
allbus2018 %$%
plot_frq(age, weight.by = wghtpew, type = "violin", show.values = F)
Plot_likert()
Um Häufigkeitsverteilungen verschiedener Likert-Items im Vergleich zu darzustellen bietet das sjplot-Paket mit der plot_likert Funktion eine sehr praktische Lösung an. Wie bei der vorherigen Funktion können über diverse Argumente die Grafik entsprechend den eigenen Vorstellungen angepasst werden. Auch hier bieten die aufgeführten Beispiele erste Orientierungen, welche Möglichkeiten bestehen.
Syntax:
# Ohne Pipe
plot_likert(datensatz$variable1, weight.by = datensatz$gewicht)
# Mit Pipe
# Nicht gut zu handhaben!Beispielcode:
# Grafik zur Verteilung von Ausprägungsmerkmalen bei Likert-Items
plot_likert(allbus2018[c("im19", "im20", "im21", "id01")], grid.range = c(.8, .8),
wrap.legend.labels = 11, wrap.labels = 12, values = "sum.inside",
show.prc.sign = T, weight.by = allbus2018$wghtpew)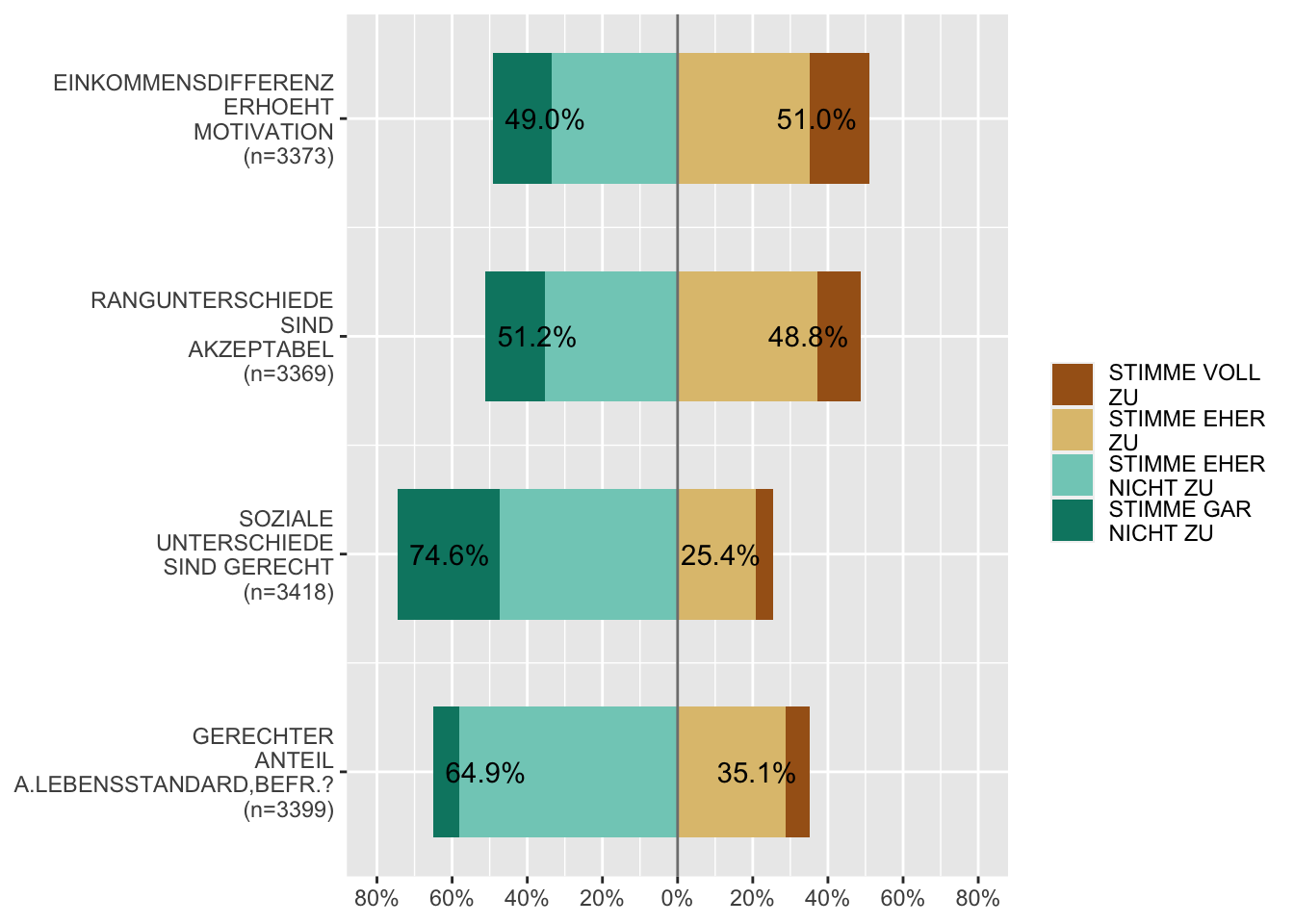
# Grafik zur Verteilung von Ausprägungsmerkmalen bei Likert-Items nach Komponenten
plot_likert(allbus2018[c("im19", "im20", "im21", "id01")], c(1,1,2,2),
grid.range = c(1.1, 1.1), values = "sum.outside",
show.prc.sign = T, weight.by = allbus2018$wghtpew, legend.pos = "none")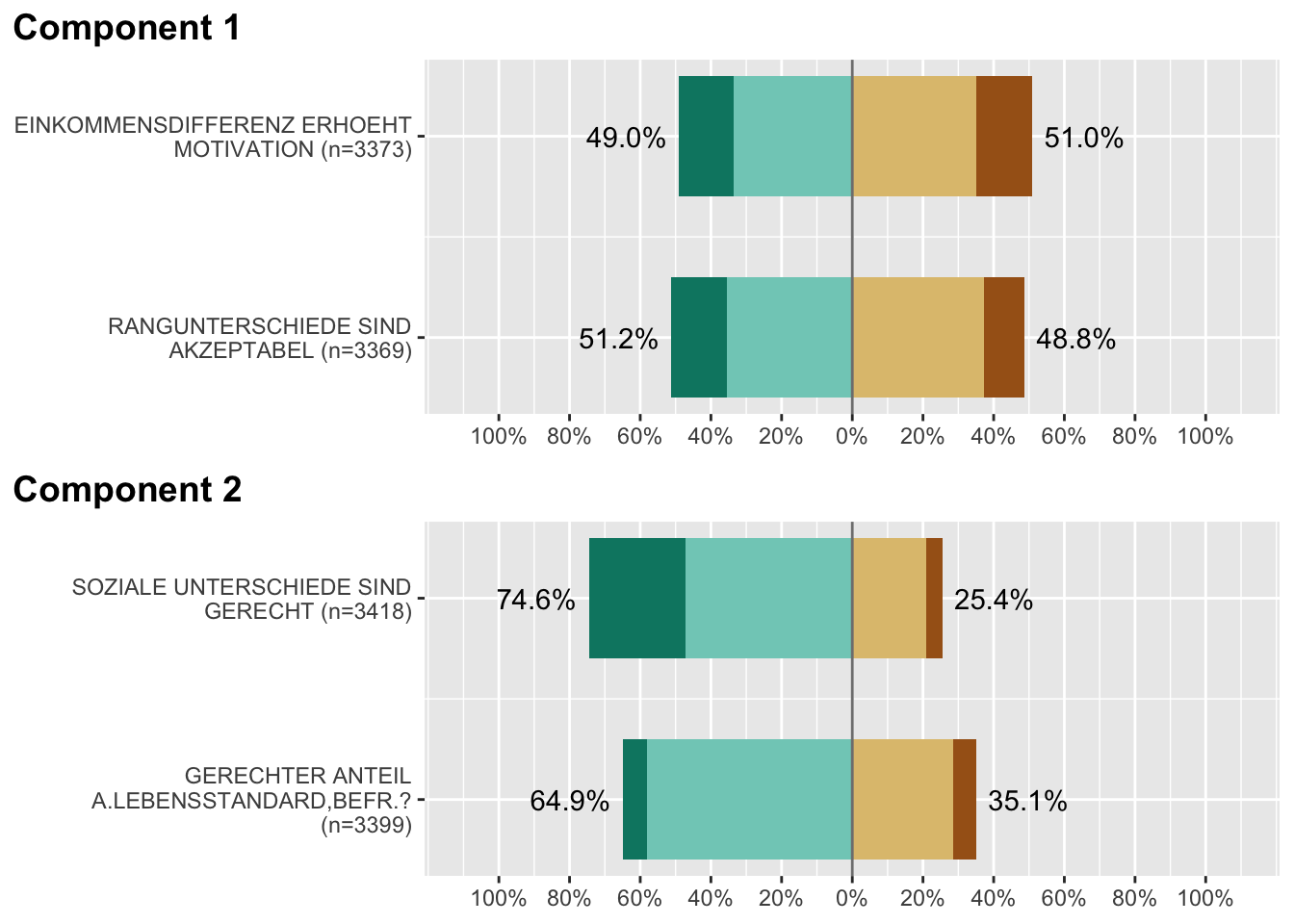
Plot_stackfrq()
Mit der plot_stackfrq() Funktion können Balkenschichtungsdiagramme erstellt werden.
Syntax:
# Ohne Pipe
plot_stackfrq(datensatz$variable1, weight.by = datensatz$gewicht)
# Mit Pipe
# Nicht gut zu handhaben!Beispielcode:
# Verteilung von Ausprägungsmerkmalen in einem Balkenschichtungsdiagramm
# Farbauswahl mit RColorBrewer::display.brewer.all()
plot_stackfrq(allbus2018[c("im19", "im20", "im21", "id01")],
weight.by = allbus2018$wghtpew, expand.grid = T, geom.colors = "Greens",
wrap.labels = 12, wrap.legend.labels = 11)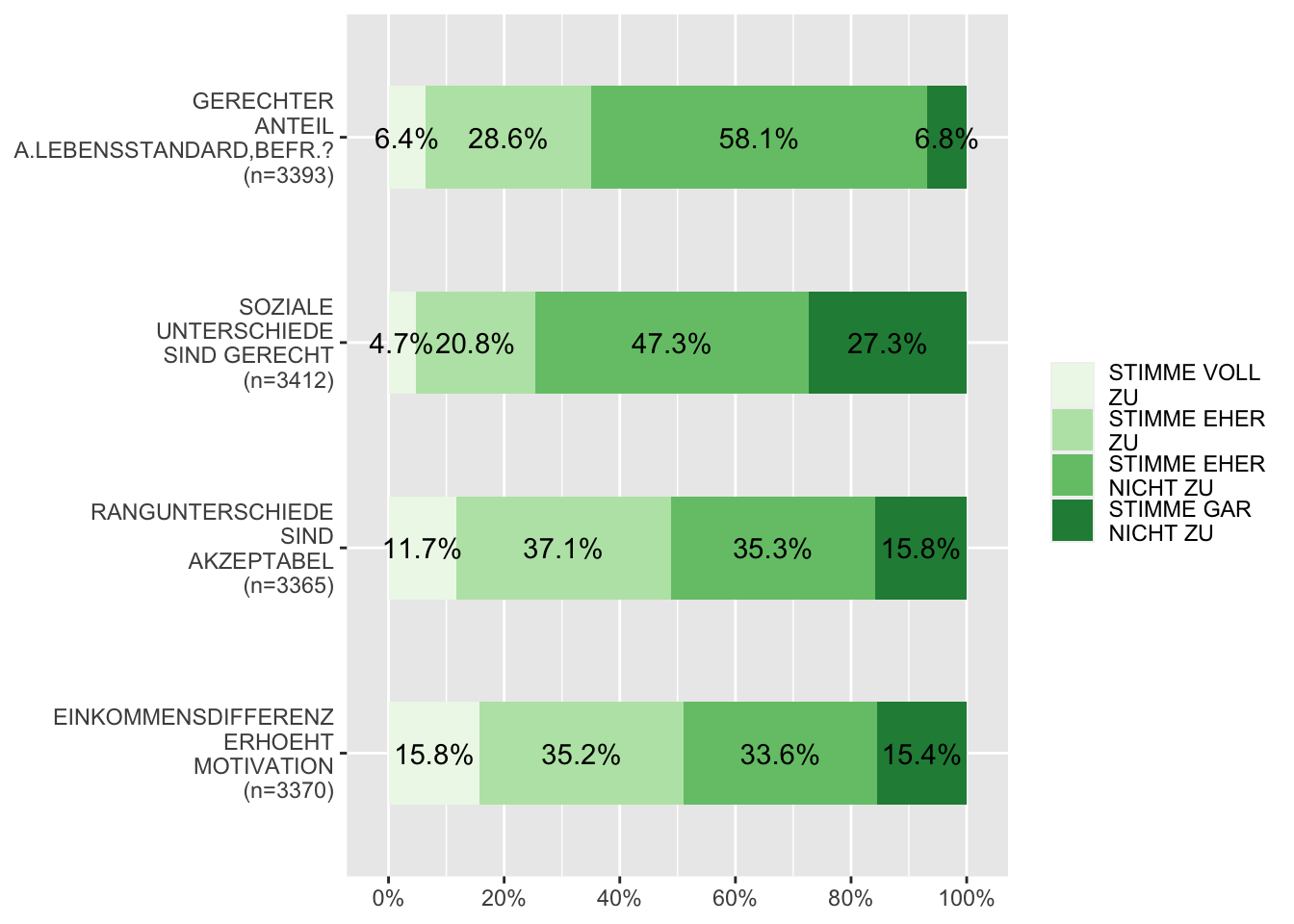
Plot_grpfrq()
Um die Häufigkeitsverteilung für verschiedene Gruppen im Vergleich abzubilden, verwenden wir die Funktion plot_grpfrq(). Diese Funktion bietet mit dem Argument show.summary auch an, die Chi-Quadart Statistiken in die Grafik zu integrieren. Auch für diese Funktion bieten die aufgeführten Beispiele einen ersten Überblick über die verschieden Möglichkeiten.
Syntax:
# Ohne Pipe
plot_frq(datensatz$variable1, datensatz$gruppenvariable, weight.by = datensatz$gewicht)
# Mit Pipe
# Achtung! %$% Operator
datensatz %$%
plot_frq(variable1, gruppenvariable, weight.by = gewicht)Beispielcode:
# Verteilung Alter (age) nach Geschlecht (sex) und Statistiken
allbus2018 %$%
plot_grpfrq(age, sex, weight.by = wghtpew, show.values = F, type = "line",
show.summary = T, summary.pos = 1)
# Verteilung Leistungsprinzip (im19) nach Schichtzugehörigkeit (id02)
allbus2018 %$%
plot_grpfrq(im19, id02, weight.by = wghtpew, show.values = F, type = "boxplot")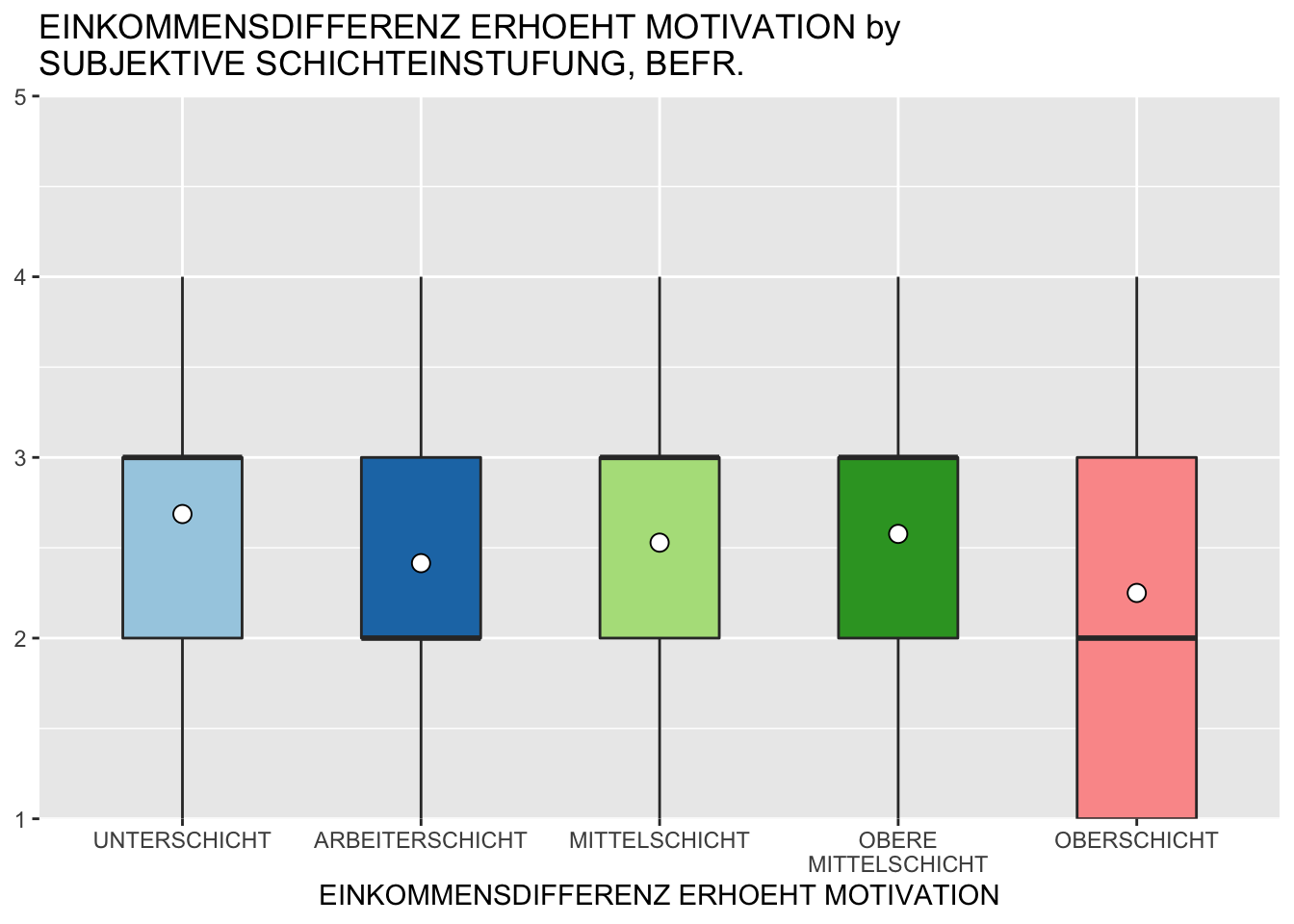
# Verteilung Leistungsprinzip (im19) nach Geschlecht (sex) und Statistiken
allbus2018 %$%
plot_grpfrq(im19, sex, weight.by = wghtpew, type = "bar", show.summary = T,
summary.pos = "1", ylim = c(0, 850))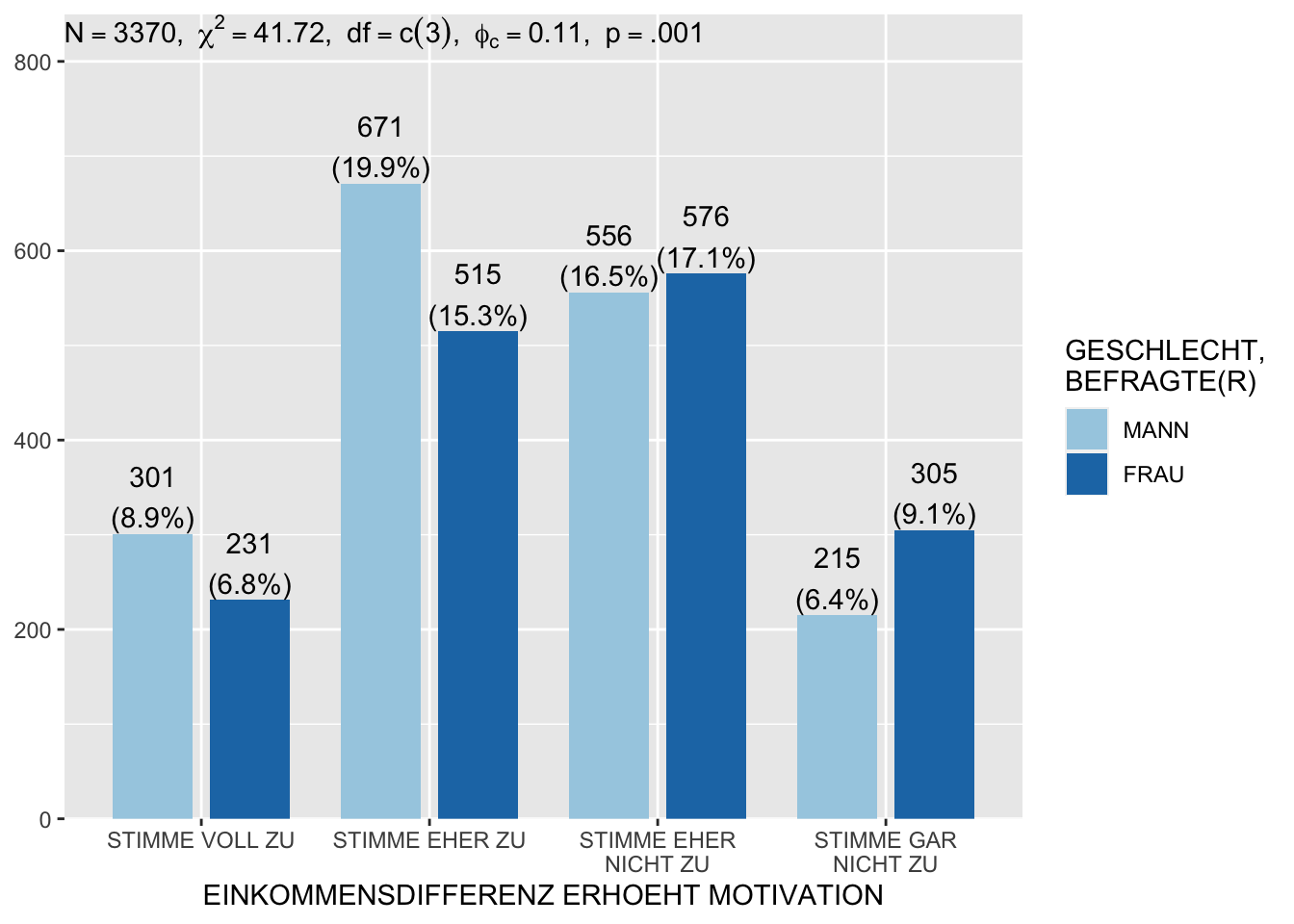
# Verteilung Leistungsprinzip (im19) nach Geschlecht (sex) und Ost West (eastwest)
# und Statistiken
allbus2018 %$%
plot_grpfrq(im19, sex, intr.var = eastwest, weight.by = wghtpew,
type = "violin", show.summary = T, summary.pos = "1")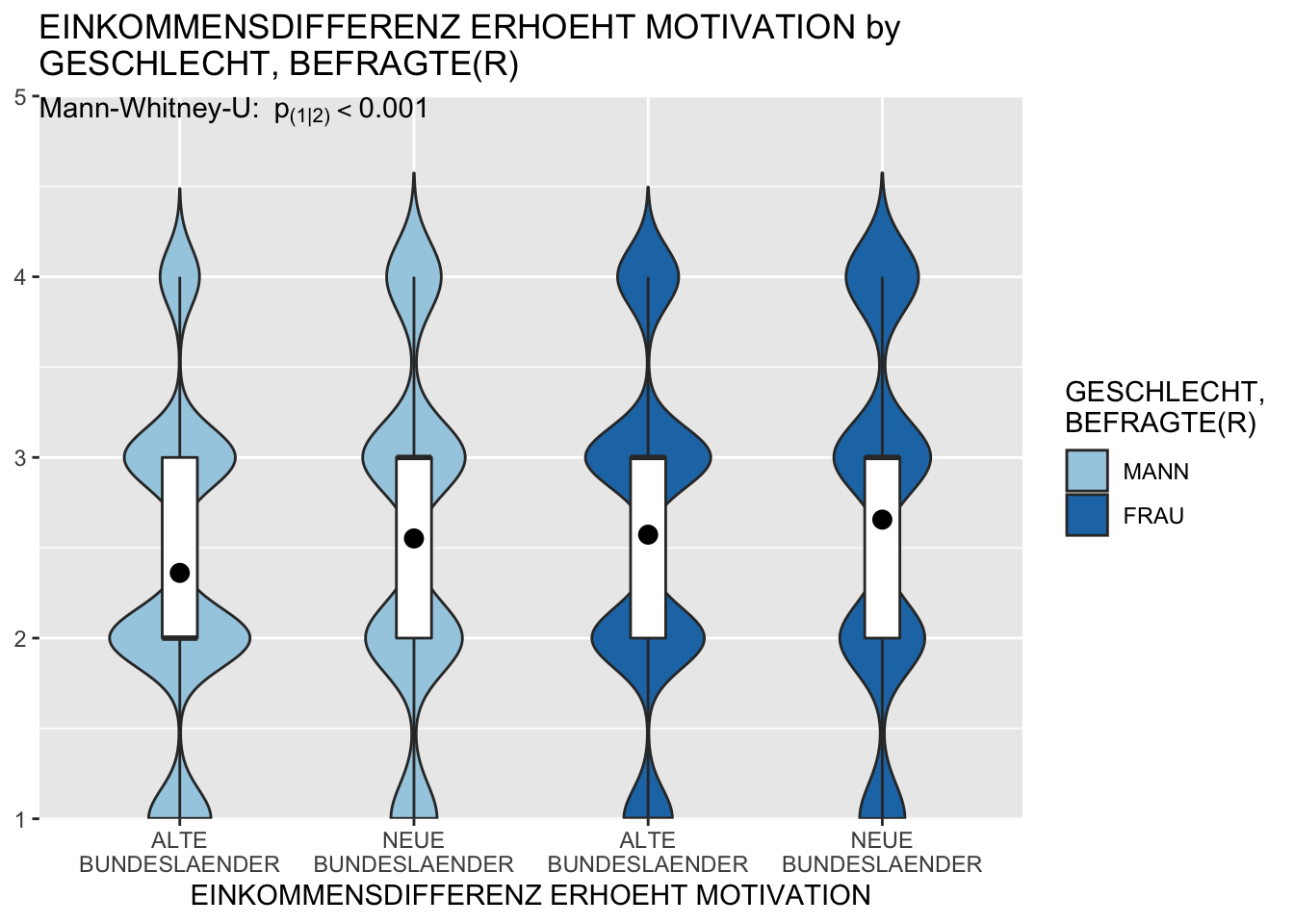
Plot_xtab()
Mit der Funktion plot_xtab() können Kreuztabellen grafisch dargestellt werden. Auch diese Funktion bietet verschiedene Möglichkeiten über Argumente die Grafik den eigenen Bedürfnissen anzupassen.
Syntax:
# Ohne Pipe
plot_xtab(datensatz$variable1, datensatz$variable2, weight.by = datensatz$gewicht)
# Mit Pipe
# Achtung! %$% Operator
datensatz %$%
plot_xtab(variable1, variable2, weight.by = gewicht)Beispielcode:
# Verteilung soziale Ungleichheit aus Makroperspektive (im21) nach Ost West (eastwest)
# und Statistiken
allbus2018 %$%
plot_xtab(im21, eastwest, weight.by = wghtpew, type = "line", show.total = F,
show.n = F, show.summary = T, summary.pos = "1")
Grid.arrange()
Wenn wir mehrere Plots erstellen, welche zusammen berichtet werden sollen, bietet es sich mitunter an, sie mit der Funktion grid.arrange() in einer Grafik vor dem Exportieren zusammen zu fassen.
Die Funktion grid.arrange() entnehmen wir aus dem Paket gridExtra.
Zur Anordnung der gewünschten Plots erstellen wir zunächst die einzelnen Plots als neues Objekt. Anschließend definieren wir mit der Funktion grid.arrange() wie diese zueinander angeordnet werden sollen.
library(gridExtra)Syntax:
# Ohne Pipe
grid.arrange(arrangeGrob(abbildung1, abbildung2))
# Mit Pipe
# Nicht gut zu handhaben!Beispielcode:
# Verteilung Alter (age) nach Geschlecht (sex) zwischen Ost West (eastwest)
p1 <- allbus2018 %>%
filter(eastwest == 1) %$%
plot_grpfrq(age, sex, weight.by = wghtpew, type = "violin", show.summary = T,
summary.pos = "1", title = "ALTER nach GESCHLECHT - WEST",
geom.colors = "Blues")
p2 <- allbus2018 %>%
filter(eastwest == 2) %$%
plot_grpfrq(age, sex, weight.by = wghtpew, type = "violin", show.summary = T,
summary.pos = "1", title = "ALTER nach GESCHLECHT - OST",
geom.colors = "Greens")
# --------
pp1 <- grid.arrange(arrangeGrob(p1, p2, nrow = 1))
pp1
#> TableGrob (1 x 1) "arrange": 1 grobs
#> z cells name grob
#> 1 1 (1-1,1-1) arrange gtable[arrange]Ggsave()
Wenn wir mit der grafischen Aufbereitung unserer Ergebnisse zufrieden sind, können wir diese mit der Funktion ggsave() exportieren.
Syntax:
# Ohne Pipe
ggsave("Grafik.png", plot = last_plot(), dpi = 300)
# Mit Pipe
# Nicht gut zu handhaben!Beispielcode:
ggsave("grid.plot.png", plot = pp1, dpi = 300)
#> Saving 7 x 5 in image